FOCUS QUESTION:
What are the special symbols and language I use when I work with sets?
SPECIFIC OBJS: By the end of the lesson, students should be able to:
3. Draw Venn Diagram to show the intersection or union of two sets.
CONTENT
A set is a group of things that have something in common. Members of a set should be written in curly braces. An empty set contains no members or elements. It is also called a null set. The cardinality of a set refers to the number of elements or members in the set. The ordinality of a set refers to the position or place a certain element/member holds in a set. A Venn diagram is a pictorial representation of sets. We can also see the relationship between different sets in a Venn diagram.

NB The rectangle represents the universal set.
ENGAGE:
Students, you would have remembered the topic Sets from grades 4 and 5. What exactly is a set?
Well you should have the following answer:
It is a group of things that have something in common. We could also say a group of things that are related.
Let's try to create some sets. Remember now that the members of a set should always be written in curly braces. Let's go!
Set P = {mangoes, pineapples, melons, cherries}
1. How could this set be described?
2. How are the elements/members common?
3. How many elements/members are in the set P?
4. What other way could question 3 be asked?
Well if you have answered the questions above correctly, then you deserve a 👍.
Let's see.
1. Set of fruits
2. They are all fruits
3. 4
4. What is the cardinality of the set P?
EXPLORE:
Ok students, I want you to read the scenario below. You are going to need two rubber bands and 6 very small pieces of paper with the following numbers written on them 2,3,4,5,6,8 (one number on each paper) for this activity. Please have them ready.
Romario was given the numbers (2, 3, 4, 5, 6, 8) to place in sets labelled as prime numbers and even numbers. He was given two rubber bands by his teacher, and asked to ensure that all the numbers were used up.
Imagine that you are Romario and use the rubber bands to show the sets.
Well by this time you should have inserted your numbers in the rubber bands as shown below.

EXPLAIN:
Can you now tell me what a set is?
What is the Venn diagram?
Can you now explain to someone why the numbers were placed in the rubber bands as shown above?
Beautiful! 2 is a prime number and it is also an even number so it was placed where the two rubber bands overlapped. Looking at the rubber bands now you will notice that 4, 6, and 8 are also even numbers but not prime numbers so they are found in the green section. The 3 and 5 are prime numbers but not even numbers so they would be found in the purple section.
EXTEND/ELABORATE:
Answer the following questions.
1.
2.

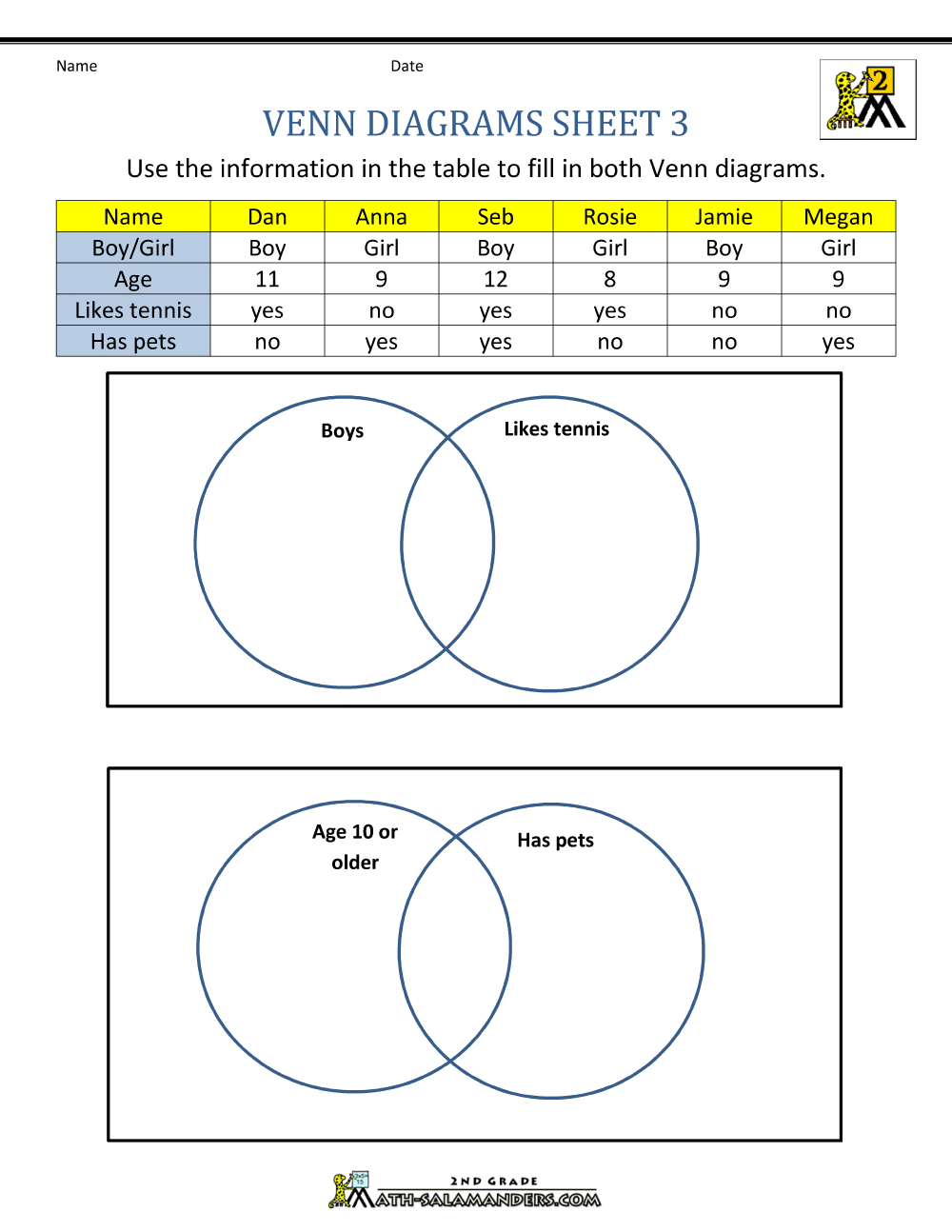
3. Use the diagram below to answer the questions that follow.

4.
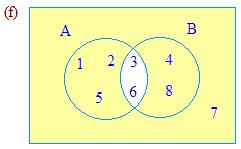
(a) What are the members of Set A?
(b) What are the elements of Set B?
(c) 7 forms part of the __________________________ set.
(d) What is A Ո B?
(e) What is A Ս B?
(f) What is the cardinality of Set A?
5.
Consider the two sets below.
Set C = { a, b, d, g, k, y}
Set N = { c, d, k, w}
FOLLOW UP PRACTICE EXERCISES
Activity 11
Grade: 6
Duration: 1 hour
Topic: Sets – Venn Diagrams
Objectives:
By the end of the lesson, students should be able to:
-
Associate the members of a set with the properties of that set.
-
Name and list members in the intersection (∩) or union (∪) of two sets.
-
Draw Venn Diagrams to show the intersection or union of two sets.
✅ Materials Needed
Flashcards or cutouts with category items
Venn diagram handouts
STEM connection video or chart (optional)
Markers, pencils
Exit ticket slips
Chromebooks, teacher's blogsite Projector
Flashcards or cutouts with category items
Venn diagram handouts
STEM connection video or chart (optional)
Markers, pencils
Exit ticket slips
Chromebooks, teacher's blogsite Projector
🌟 5E Model Lesson Plan
1. Engage (10 minutes)
Activity: Set Sort & Predict
-
Present students with a mixed collection of items (words or pictures on flashcards or digital images): e.g., types of fruits, animals, shapes, even/odd numbers.
-
Ask: “What’s one way we could group these items?”
-
Let students sort and explain their choices.
-
Transition into discussion:
-
“In math, we use sets to group things that have something in common.”
-
Introduce the symbols:
-
∈ (is an element of)
-
∪ (union)
-
∩ (intersection)
-
{} (curly brackets for listing set elements)
-
Ø or {} (empty set)
-
-
STEM Integration:
Discuss data classification in science and how scientists sort living things into different groups using common characteristics—just like math sets!
2. Explore (10 minutes)
Activity: Real-World Set Investigation
-
Divide class into pairs.
-
Give them two categories (e.g., Students who like football and Students who like music).
-
Students survey 6–8 classmates and create sets:
-
Set A: Students who like football
-
Set B: Students who like music
-
-
Guide them to identify:
-
A ∪ B (students who like football or music)
-
A ∩ B (students who like both)
-
Differentiation:
-
Provide pre-filled templates with names for students needing support.
-
Let fast finishers create their own categories for new sets.
3. Explain (15 minutes)
Activity: Teacher Modeling & Discussion
-
Use a whiteboard or projector to show:
-
How to define a set using {} and list members.
-
How to draw two overlapping circles (Venn Diagram).
-
How to fill in each section of the Venn Diagram based on given sets.
-
Introduce and model use of ∪ and ∩ symbols.
-
-
Example:
-
Set A = {2, 4, 6, 8}
-
Set B = {4, 5, 6, 7}
-
A ∩ B = {4, 6}
-
A ∪ B = {2, 4, 5, 6, 7, 8}
-
4. Elaborate (15 minutes)
Activity: STEM Connection & Applied Problem-Solving
-
Pose a problem:
-
“A class of 20 students was surveyed. 12 like math, 8 like science, and 5 like both.
-
Draw a Venn Diagram.
-
How many like only math? Only science? Neither subject?”
-
-
-
Students work in small groups to solve and present.
-
Discuss how understanding sets helps in data analysis, scientific classification, and engineering design.
Differentiation:
-
Use color-coded circles and name tags for visual learners.
-
Offer sentence starters or math symbols reference charts for language learners or struggling readers.
5. Evaluate (10 minutes)
Three-Tier Evaluation Activity
Students complete activities based on readiness:
| Tier | Task | Sample Question |
|---|---|---|
| Tier 1 (Basic) | Match set symbols to meanings and draw simple Venn diagrams for pre-made sets. | What is the union of Set A = {1, 2, 3} and Set B = {3, 4}? |
| Tier 2 (Intermediate) | Given two sets, list the intersection and union, and represent them on a Venn Diagram. | Draw a Venn Diagram and shade A ∩ B for A = {a, b, c}, B = {b, c, d}. |
| Tier 3 (Advanced) | Solve a real-world problem involving set relationships, and interpret results. | In a survey, 18 like basketball, 10 like football, and 6 like both. How many like only basketball? Draw a Venn Diagram to represent the data. |
Exit Ticket (Alternative/Extension):
-
Write one sentence using each of the following: ∈, ∪, ∩.
-
Challenge: Describe a situation outside of math where sets and Venn Diagrams can be used.
📌 Notes on STEM & Differentiation
-
STEM Integration: Use science or technology examples for set grouping (e.g., classifying rocks, filtering data in apps).
-
Differentiation Strategies:
-
Visual aids for struggling learners
-
Real-world contexts for relevance
-
Tiered evaluation to meet all learners' levels
-



No comments:
Post a Comment