SETS/ DISJOINT

DISJOINT SETS

FOCUS QUESTION: 

What are the special symbols and language I use when I work with sets?

 

SPECIFIC OBJS. By the end of the lesson students should be able to:

1.  Name and list members in the intersection or union of two sets.

2.   Define “disjoint sets”.

 CONTENT SUMMARY

In other words, the two sets have no common elements/members.

ENGAGE

Students  I want you to examine the Venn diagrams below, then tell me what is the difference between the two representations of Sets A and B.

Why was there an overlap in the first Venn diagram?

Why was there no overlap in the second Venn diagram?

EXPLORE

Well by now you should have realized that the first  two sets had "a" and "b" as common elements and so there was an overlap of the two circles to show the elements common to both sets.

On the other hand, the second Venn diagram depicted two separate circles because the elements or members of the two sets A and B had no common elements.

Now this type of set is referred to as a  DISJOINT SET.

You can watch this video clip to glean more information.

EXPLAIN

Now can you explain what a disjoint set is?

EXTEND

Write a scenario that would be represented by disjoint sets.

EVALUATION

1. Examine the diagram below carefully, then answer the question that follows:

Which of the following represents the Venn diagram above?

(a) U= {1, 2, 3, 4, 5, 6, 7, 8, 9}

      A={1, 2, 5, 6}

      B={3, 9}

(b) U=(4, 7, 8}

      A={1, 2, 6, 5, 8}

      B={3,4,9}

(c) U={ 7, 8, 9}

      A={1, 2, 3, 4, 5, 6, 7, 8, 9}

      B={3,  4, 7, 8}

2. Consider the sets below:

    M={odd numbers between 0 and 10}

    V= {prime numbers between 1 and 12}

                      and

    J= {1, 4, 6, 13}

   K= {2, 5, 7, 10}

Draw the two Venn diagrams to represent the sets. Which is the example of a disjoint set?

Follow up Practice Exercises

Activity 1

Activity 2

Activity 3

Activity 4

Activity 5

Activity 4

🧠 Lesson Overview

• Grade: 6

• Subject: Mathematics

• Theme: Disjoint Sets

• Focus Question: What are the special symbols and language I use when I work with sets?

• Duration: 1 hour

• Objectives:

  1. Name and list members in the intersection or union of two sets.

  2. Define “disjoint sets.”

---

🔎 5E Lesson Plan

1. Engage (10 minutes)

Activity: Set Sort and Compare

• Present students with two different bags (real or virtual) containing labeled cards:

  • Bag A: {apple, banana, orange}

  • Bag B: {carrot, potato, cabbage}

• Ask:

  • What do you notice about the items in both bags?

  • Are there any items that appear in both bags?

• Guide students to conclude there are no common elements → lead into the concept of disjoint sets.

STEM Integration: Technology — Use an online Venn diagram simulator (e.g., mathisfun.com) to drag and drop items interactively.

---

2. Explore (10 minutes)

Activity: Hands-On Set Building

• In small groups, students receive two sets of cards with mixed elements (numbers, letters, or objects).

• Task:

  • Create two sets that intersect (e.g., Set X: {1, 2, 3}, Set Y: {3, 4, 5})

  • Then create two disjoint sets (e.g., Set A: {a, b}, Set B: {x, y})

• Students draw Venn diagrams to represent these relationships.

Differentiation:

• Tier 1: Teacher support with word cards and visual cues.

• Tier 2: Moderate scaffolding with guiding questions.

• Tier 3: Independent creation of set examples with symbols.

---

3. Explain (15 minutes)

Mini-lesson:

• Define:

  • Set: a group of objects/elements.

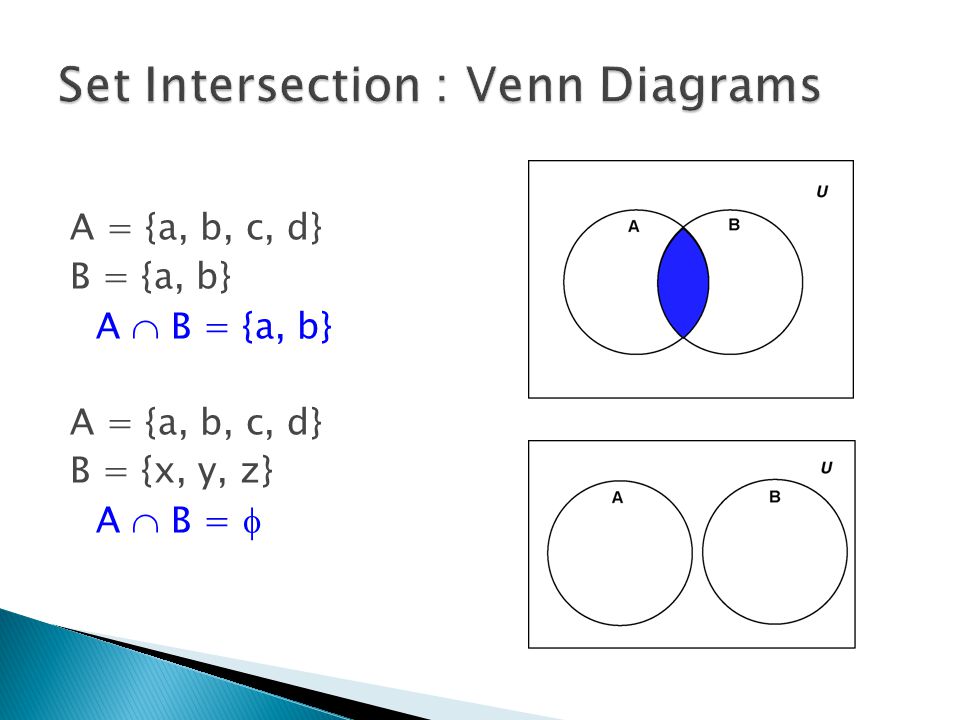
  • Union (∪): all elements from both sets.

  • Intersection (∩): common elements.

  • Disjoint sets: sets with no elements in common.

• Introduce symbols:

  • ∩ = intersection

  • ∪ = union

  • ∅ = empty set

• Use board/visual to show:

  • Set A = {1, 2, 3}, Set B = {4, 5, 6}

  • A ∩ B = ∅ → Disjoint Sets

• Guide students in recording definitions and drawing examples.

STEM Integration: Math Language + Logical Thinking (Computational Science: Classifying/Grouping Data Sets)

---

4. Elaborate (15 minutes)

Activity: STEM Challenge – Sorting Data

• Scenario: Students are software designers building a filter for a streaming platform. They must:

  • Create two sets of user preferences (e.g., Set A: {Action, Sci-Fi}, Set B: {Romance, Drama})

  • Determine if the sets overlap or are disjoint.

  • Represent them using Venn diagrams and write:

    • A ∩ B = ?

    • A ∪ B = ?

Differentiation:

• Visual learners: Use color-coded diagrams.

• Kinesthetic learners: Use set circles with physical cut-out images.

• Advanced learners: Add a third set and analyze.

---

5. Evaluate (10 minutes)

Three-Tier Evaluation Activity:

Tier	Activity	Evaluation Focus
1	Match sets using cut-outs or visuals to identify if they are disjoint, overlapping, or equal	Recognize disjoint sets visually
2	Given Set A and Set B, write A ∪ B and A ∩ B. Indicate if the sets are disjoint	Apply union and intersection correctly
3	Write a real-life example of disjoint sets (e.g., types of animals vs. types of vehicles) and represent it with a labeled Venn diagram	Apply understanding to real-world context

---

✍️ Summary / Exit Ticket (Wrap-up)

• Ask: “What does it mean if two sets are disjoint?”

• Students write their own sentence using the word disjoint and draw a quick Venn diagram of disjoint sets.

---

📚 Materials & Resources:

• Venn diagram chart

• Cut-out set items (images or words)

• Markers, chart paper, or interactive whiteboard

• Tablets/laptops (if available) for online Venn simulation

---